Target Trial Emulation in Practice
Published: 2024-08-08
Define your question as a target trial protocol
Define your question as a target trial protocol
In target trial emulation, the research question will be in the form of a trial protocol and a causal contrast or effect measure. The effect is defined and identified using a causal theory of choice – many are basically equivalent – and estimated using statistical methods of choice. (Currently I like counterfactuals and single-world intervention graphs [SWIG], and Bayesian models in probabilistic programming languages inferred with MCMC algorithms).
Familiarity with trials is very helpful but the basic elements are fairly simple:
Eligibility criteria are variables and required values that restricts the study population. In an actual trial these criteria may be decided so that the population has a maximal chance to benefit from the treatment, or perhaps so that the population is the same as the population already treated in most practical settings. In observational settings, eligibility may additionally need to depend on data availability factors.
Treatment strategies (including control treatments). A full treatment strategy should be sufficiently well-defined so that wildly different treatments are not compatible with it. In other words, all treatment labelled with the same value, say \(\bar{a} = \bar{1}\), should have the same effect. The strategy may take into account the quality of treatment, reasonable rules to change or stop the treatment, the use of other concurrent treatments, and so on, depending on the interventions of interest.
Treatment assignment in trials is randomized and possibly blinded from study participants. Blinding may be impossible to emulate so the target trial will be necessarily unblinded. But in principle we could start from a double-blinded target trial as our target and only later change it as we realize that we cannot emulate this feature using our data sources.
Time zero is usually when the follow up of outcomes starts. In trials this is aligned with treatment assignment and often the start of treatment itself (if there is no grace period).
End of follow-up is the time after which measurement of outcomes is stopped for different reasons, for example, because the unit is no longer at risk of the outcome event of interest.
Primary outcome is important in trials for many reasons. In general, the trial is designed from scratch to estimate the effect on the primary outcome which makes it reliable.
Obviously (and importantly), trials are designed and run over time and so contain different kinds of dates, observation windows, and visit schedules such as
date extraction date, which tells when a live data source was queried for analysis
source data range, showing the date range that the data source covers for certain information (such as healthcare encounters)
cohort entry or index date, which is the date of treatment assignment in trials and defines time zero
exclusion assessment windows, before time zero, during which eligibility criteria need to be measured and met
covariate assessment windows, before time zero, during which covariates like confounders and effect modifiers need to be measured
exposure assessment windows are needed when cohort entry (time zero) is not defined by exposure (treatment assignment), a run-in period is used to select adherent people, exposure is time-varying, and so
outcome washout window, that is, the interval before time zero during which outcomes are not allowed
exposure washout window
run-in period
grace period, which is the interval between assignment and start of treatment (quite common in practice)
induction/latent/incubation period, during which a cause doesn't yet have an effect on the outcome even though exposure has happened (the term comes from infections)
follow-up window, starting after time zero and ending to a censoring event, during which an effect on the outcome is assumed possible and outcomes are measured
outcome event date
When the trial protocol and the variables are defined, the causal contrast or effect measure can be defined precisely. Some options include:
Compare outcomes under interventions on treatment assignment \(Z\) and remaining uncensored, like \(\Pr[Y^{z=1, c=0} = 1] - \Pr[Y^{z=0, c=0} = 1]\), called the intention-to-treat effect (effect of assignment).
Compare outcomes under interventions on both assignment and treatment, like \(\Pr[Y^{z=1,a=1,c=0} = 1] - \Pr[Y^{z=0,a=0, c=0} = 1]\), called a per-protocol effect (effect of adherence to assignment).
Compare outcomes under interventions on treatment and some of its intervenable mediators, such as \(E[Y^{a=1,m=0}] - E[Y^{a=0,m=0}]\), called a controlled direct effect. If the mediator is not a well-defined intervention, one might consider separable components of the treatment, \(N\) and \(O\), so that the effect of \(N\) is mediated by \(M\), in which case one could consider, for example, a total indirect effect \(E[Y^{a=1}] - E[Y^{a=1, M^{a=0}}]\) which in the language of the separable components would be \(E[Y^{n=1,o=1}] - E[Y^{n=0,o=1}]\) which is the effect through \(M\).
Causal diagrams (like SWIG) can be used to clarify the effect of interest and how it is identifiable in the target trial.
Finally, a data analysis plan for estimating the causal contrast of interest – given data from this target trial – is written. Note that this plan is made blind to any results from real data and will serve as a template for the emulation analysis plan. Problems arising later with real data will be ironed out in a series of sensitivity analyses.
As a fan of Bayesian analysis with probabilistic programming languages, a few points on model building are in order here:
Since data analysis is programmatic it should follow simple software engineering principles. Version control, testing, reproducibility, readability, and modularity are important. Often projects should consist of a series of scripts in programming languages (and text files in a markup language and raw input data files – outputs don't need to be tracked).
Models can be made fully or partially generative. It is common not to model at least some values (like sample size and baseline regression inputs) but it might be good to make the model as generative as warranted by domain knowledge. 'Generativeness' aids model checking.
Modelling is usually best to start from an initial simple model (template) that is commonly used or has been used before in a similar problem (textbook, articles, etc). The initial model provides the basic modules that can be modified later as we think more deeply about the assumptions. Later we attempt building the most complex custom model that is designed from first principles and made as flexible as possible given the domain knowledge and available data. A good model can be often found at the middle.
Parameters should be made interpretable. Standardization is often useful which here means subtracting a natural center and dividing by dispersion. Interpretable parameters can be given more reasonable priors such that nonsensical values can be easily assumed unlikely.
Predictions before inference should make some sense. Prior predictive checking shows how the choice of priors affects what kind of data the model generates. The combined meaning of multiple priors can be sometimes counterintuitive, even as far as generating nonsensical data. Detecting such problems helps make the prior and model more reasonable.
Models should be able to fit simulated data and recover known parameter values. Samples from the prior predictive itself are one useful test case. This can also give a rough idea of the sample sizes necessary for useful estimates.
Model fitting needs to be monitored. A standard method to fit probabilistic models is by using Hamiltonian Monte Carlo algorithms (like NUTS). The fitting process can be checked by sampling multiple independent Markov Chains and looking at their convergence, mixing, and effective sample sizes.
Computational problems can be often fixed by improving the model – the fitting process is also a kind of model check. This includes adding or removing complexity and flexibility, using more or less informative priors (including hard constraints), and reparametrization. Sometimes problems can be revealed by visualizing intermediate quantities and predictions with the failing posteriors. If priors cannot be made more informative, external informative data can smoothen out the posterior geometry in a similar way. After working on the model and data, it is possible to change or finetune the inference algorithm.
Plan how to emulate each element of the target trial protocol
Plan how to emulate each element of the target trial protocol
Even though the target trial is supposed to define our goal, it is not useful as a goal if it's too far from realistic emulation. Even the first guess at a target trial (a question) of interest can't be too fanciful as we eventually need to emulate it with real data.
For most features of the trial, emulation is just a matter of finding relevant data sources that match or approximate the measurements that would've been done in the target trial. If data sources are not found, the target trial (question) needs to be modified to match the available data (or the project is stopped). This is the case for eligibility, treatment, time zero, end of follow up, and primary outcome – all of which need to match the target trial. A precise description of variables is needed, that is, how each target trial element has been measured (or predicted) – comparing an ideal variable in a target trial to the available data is a good way to clarify sources of error. In general, evaluating the reliability of observational 'found' data (and prediction models) is crucial.
Placebo treatments may be possible to emulate using other treatments that can be assumed to be inert to the outcome of interest. For example, in drug research, other unrelated drugs have been used as placebos. However, it is often quite unclear how close any candidate placebo-emulator actually is to a real placebo used in a plasebo-controlled trial. Anyway, placebos are rarely used without blinding and other active comparators may be more informative for practice.
Treatment assignment is a trial concept that is not usually available in observational data. In trials, assignment is basically a treatment plan, so in principle, different treatment plans (e.g. prescriptions) might be used to emulate treatment assignment. However, many trials assign and start the treatment at the same time, so the first treatment can be used as an analog for assignment. As such, the intention-to-treat effect can be emulated by comparing outcomes under interventions on initiating treatment and remaining uncensored, such as \(\Pr[Y_k^{a_0 = 1, \bar{c} = \bar{0}} = 1] - \Pr[Y_k^{a_0 = 0, \bar{c} = \bar{0}} = 1]\) up to time \(k\), often called the observational analogue of intention-to-treat. Note how \(a_0 = 1\) is used instead of the missing \(z = 1\).
Per-protocol effect emulation is possible by assuming exclusion restriction which means that assignment affects outcome only through the treatment. So, a per-protocol effect could compare outcomes under interventions on full treatment and remaining uncensored, such as \(\Pr[Y_k^{g_1, \bar{c} = \bar{0}} = 1] - \Pr[Y_k^{g_0, \bar{c} = \bar{0}} = 1]\) up to time \(k\).
Randomization of the treatment assignment can then be emulated using methods of causal inference. Hypothetically, if all relevant confounders (a sufficient adjustment set) were known and measured precisely, the treatment would be effectively randomized within levels of the confounders (g-formula). Alternatively, special causal structures may be searched for and used to emulate randomization. So, emulating randomization usually starts from making causal assumptions on a causal diagram (like a SWIG) and then finding data to block the backdoor paths in analysis. This is done to assume exchangeability. Again, measurement (or prediction) of counfounders needs to be sufficiently reliable, complete, and precise.
All assumptions needed to identify counterfactual measures using observable data is slightly more complicated. Here's a summary.
The most generally useful conditions for identifying causal effects are exchangeability, positivity, and consistency. These would be fulfilled in a conditionally randomized experiment which we try to emulate. More specifically, we need to assume that
At every time interval \(k\), the outcome when everyone receives an intervention \(Y^g\) is independent (d-separated) from treatment at \(k\) and censoring at \(k+1\), conditional on confounders, past treatment, and being uncensored at \(k\). This is done by assuming a certain causal structure (like SWIG) and using the backdoor criterion to arrive to a sufficient adjustment set.
At every time interval \(k\), it is possible to observe all treatments at \(k\) while remaining uncensored at \(k+1\) for all joint values of confounders and past treatment. In missing spots it may be assumed while modelling that the missingness is random rather than a violation.
If the observed history of treatment \(\bar{A}_K\) is consistent with intervention while remaining uncensored to \(K+1\), the observed outcome \(Y\) is consistent with the counterfactual outcome under the intervention \(Y^g\) and the observed confounder history is consistent with the counterfactual confounder history under the intervention. Consistency requires sufficiently well-defined counterfactual interventions and correspondence between counterfactual and observed intervention.
Less commonly, it may be possible to avoid assuming 'no unmeasured confounding' by leveraging known complete mediators of random assignment (instrumental variables), mediators of effect (frontdoor formula), and mediators of unmeasured confounding (proximal inference). Each method assumes a certain causal structure and possibly many additional assumption. I won't cover these methods in this post.
For example, common sources of confounding in medicine include age and sex, ethnicity and socioeconomic factors, comorbidity and outcome severity factors, co-treatment and health behaviour factors, and healthcare use. In general, confounders can be identified by thinking about the most influencial factors that affect choice of treatment and risk of outcome or that are effects of such factors (or maybe just predictors). Note that misclassifying colliders or instrumental variables as common causes will cause bias (!) – domain knowledge on the causal graph is important.
A data analysis plan for the emulation is then specified. It is usually similar to the target trial analysis plan except for the variables and methods needed to emulate randomized treatment assignment.
Finally, when a feasible target trial and emulation protocol has been found, the protocols should be preregistered before they can be affected by results.
Perform pre-inference checks
Perform pre-inference checks
Before proceeding to inference, avoidable errors should be screened. This includes sufficient sample size (precision), distribution of baseline variables by treatment (positivity violations), distribution of variables by adherence to assignment (informative censoring), and possible model misspecification indicators. The model and protocol can be still modified while the analyst is blinded with respect to primary result – but the changes need to be reported as amendments to the original plan.
In Bayesian analysis, posterior predictive checking can show how close the generated data from the fitted model is to the real data. Often comparing visualizations of datasets side-by-side is informative about severe misspecification – any measures of interest on the real and predicted data can be compared. Measures of predictive accuracy can be used to summarize the overall predictive performance but it is crucial to remember that predictive accuracy is not the goal of causal inference nor modelling in general. To make the predictions more realistic (out-of-sample), cross validation is necessary (such as with PSIS-LOO).
Plan post-inference checks
Plan post-inference checks
What is the effect of plausible study changes and assumption violations on the result? A plan to evaluate the robustness of the primary result should be prespecified.
In principle, any choice in the study pipeline could be varied to assess its effect on the result. The more arbitrary the decision, the more its effect on results should be assessed.
The effect of potential measurement error, unmeasured confounding, and selection bias can be explored through modelling and simulation. Net bias can be also assessed by replicating published RCTs or by using negative (or positive) control variables, that is, by replicating other well-known effects or associations.
In Bayesian modelling, the following has been recommended:
Sensitivity to data points is revealed in cross validation since this method effectively fits the model on many subsets of data and these models can be compared. Difficult-to-predict data points should be inspected.
Sensitivity to priors can be understood in many ways. A simple way is to measure how much the priors shrink during fitting – if the prior is close to the posterior, prior influence is high and data uninformative. For a small number of models, priors can be just changed and the models refit and compared.
Sensitivity to modeling decisions in general can be seen by reporting target estimates (like some parameters) from all model variants side-by-side – perhaps ordered from the simplest to the most complex (related concept is multiverse analysis). This helps better understand the primary model in reference to other models, as well as all the other models. It also prevents some cherry picking error.
Perform inference and checks and report
Perform inference and checks and report
Planning and pre-specification is key to minimize work at the inference phase. This way study design is not affected by results which reduces bias in the final result. However, iterative model improvement may be still needed and this is fine when it is not directed at certain metrics and it's reported as amendments to the original plan.
Toy example
Target trial specification
Eligibility criteria are measured over some windows before treatment and only units with \(S_0 = 1\) are selected to the analysis.
Treatment strategies: \(A_k = 1\) means receiving a specific treatment during \(k\) and \(A_k = 0\) none of it. We compare two treatment strategies involving \(A\): always one \(g_1\) for all and always zero \(g_0\) for all.
Treatment assignment: randomized unblinded assignment \(Z\) to strategy \(g_1\) or \(g_0\).
Time zero: assignment to treatment strategy at \(k = 0\).
End of follow-up: Outcome or study end (no censoring).
Primary outcome: \(Y = 1\) is a survival outcome during follow-up.
Causal contrast: \(\Pr[Y_k^{\bar{z}=\bar{1}, g_1} = 1] - \Pr[Y_k^{\bar{z}=\bar{0}, g_0} = 1]\) where \(k\) means risk of \(Y\) up to time \(k\) (per-protocol).
Assuming exchangeability, positivity, and consistency as well as adherence, exclusion restriction, and no censoring for simplicity (and some other assumptions), we can identify...
\(\Pr[Y_k^{\bar{z}, g} = 1] = \Pr[Y_k^{\bar{z}} = 1] = \Pr[Y_k = 1 | Z = z] \Rightarrow\) \(1 - \Pr[Y_k = 0 | Z = z] \Rightarrow\) \(1 - \prod_{m=1}^{k} \Big( 1 - \Pr[Y_m = 1 | Y_{m-1} = 0, Z = z] \Big)\)In a primary analysis plan, the hazard \(\Pr[Y_m = 1 | Y_{m-1} = 0, Z = z]\) is estimated with a logistic regression model on person-time data. Risk up to \(k\) is predicted for \(Z=1\) and \(Z=0\) and subtracted. The mean and 2.5-97.5% percentiles of the posterior are computed.
Emulation
We pretend the data contains accurate and consistent measurements of treatment \(A\) and outcomes \(Y\) over time intervals \(k\) for eligible units as in the target trial. End of follow-up is at the outcome or end of study. We emulate the per-protocol effect as \(\Pr[Y_k^{g_1} = 1] - \Pr[Y_k^{g_0} = 1]\) assuming assignment similar to the target trial.
The SWIG is difficult to draw at this point as there are way too many arrows. But to get the idea, I sketched the graph below.
We can at least see how a time-varying confounder (in red) can generally open backdoors all over the place. This is the reason why we usually need to adjust for the whole history of the confounder. The confounders also become counterfactual through treatment-confounder feedback so one also needs to adjust conditional on the treatment history. Blocking \(L\) and \(A\) can also block common causes of \(L\) and \(Y\) which are called \(W\) is this sketch.
Assuming exchangeability of treatment groups at each \(k\) conditional on past treatment and confounders, positivity, and consistency as well as adherence, exclusion restriction, and no censoring for simplicity (and some other assumptions), we can identify \(\Pr[Y_k^g = 1]\) using the parametric g-formula.
The g-formula for survival outcomes is the conditional survival curve standardized to the confounder distribution...
\(\sum_l \Big(\prod_{m=0}^k \Pr[Y_{m+1} = 0|Y_m = 0, L=l, A=a]\Big) \times \Pr[L=l]\)The g-formula for end-of-follow outcomes and time-varying treatments and confounders is the conditional mean outcome standardized to the confounder distribution at each time step conditional on history needed for exchangeability...
\(\sum_{\bar{l}} E[Y|\bar{A} = \bar{a}, \bar{L} = \bar{l}] \times \prod_{k=0}^K f(l_k|\bar{a}_{k-1}, \bar{l}_{k-1})\)We need a combination of these variants but it's not necessary to use this representation of the g-formula. We can also think of an equivalent process as a simulation.
The parametric (plug-in) g-formula can be estimated using simulation because a weighted average of the expectations is the same as an expectation of the expectations. The whole density distribution (marginal or conditional as above) is not necessary since samples from the distribution are enough to average over – and these samples can be either observed or simulated. This is the iterated conditional expectations (ICE) representation of the g-formula.
In the primary analysis plan, we model the outcome hazard using the same logistic regression model on person-time data adjusting for confounders. The confounders and past treatment (A, L1, L2, L3) are modelled similarly using regression models. Finally, data are simulated sequentially and the hazard estimated at each \(k\) and transformed to risk up to \(k\). The mean and 2.5-97.5% percentiles of the posterior of the risk are computed.
Data analysis
In Bayesian analysis, the model and the simulator are often the same. This makes planning the data analysis from scratch much easier.
Here's a quick and dirty implementation of the model in Julia (Turing).
@model function pooled_logit_hazard(
n::Int,
K::Int,
L1::Matrix{Union{Missing, Int}},
L2::Matrix{Union{Missing, Int}},
L3::Vector{Union{Missing, Int}},
A::Matrix{Union{Missing, Int}},
Y::Matrix{Union{Missing, Int}}
)
# Baseline covariate uncertainty.
p₁ ~ filldist(Beta(1, 1), 4)
# Global average log-odds uncertainty.
# logit(0.1) puts the center on 10% probability.
# log(10) would then spread 1SD uncertainty on 1-52% where 10 is odds ratio.
αL1 ~ Normal(logit(0.1), log(50))
αL2 ~ Normal(logit(0.1), log(50))
αA ~ Normal(logit(0.5), log(50))
αY ~ Normal(logit(0.01), log(50))
# Time-dependent adjustment on the global average.
# log(1) puts the center on (conditional) odds ratio 1 (constant over time).
# log(5) spreads 1SD uncertainty on 0.2-5 conditional odds ratio.
αtL1 ~ filldist(Normal(log(1), log(5)), 6)
αtL2 ~ filldist(Normal(log(1), log(5)), 6)
αtA ~ filldist(Normal(log(1), log(5)), 6)
αtY ~ filldist(Normal(log(1), log(5)), 7)
# Confounder and lag-1 coefficient uncertainty.
# log(1) puts the center on odds ratio 1 (conditional independence).
# log(10) spreads 1SD uncertainty on 0.1-10 odds ratio.
βL1 ~ filldist(Normal(log(1), log(10)), 2)
βL2 ~ filldist(Normal(log(1), log(10)), 2)
βA ~ filldist(Normal(log(1), log(10)), 4)
βY ~ filldist(Normal(log(1), log(10)), 7)
# k = 1
for i in 1:n
L1[i,1] ~ Bernoulli(p₁[1])
L2[i,1] ~ Bernoulli(p₁[2])
L3[i,1] ~ Bernoulli(p₁[3])
A[i,1] ~ Bernoulli(p₁[4])
leY = αY + αtY[1] +
βY[1]*A[i,1] +
βY[3]*L1[i,1] + βY[5]*L2[i,1] + βY[7]*L3[i]
Y[i,1] ~ BernoulliLogit(leY)
end
for k in 2:K
atrisk = findall((x -> !ismissing(x) && x == 0), Y[:,k-1])
length(atrisk) == 0 && break
for i in atrisk
leL1 = αL1 + αtL1[k-1] +
βL1[1]*L1[i,k-1] + βL1[2]*L3[i]
L1[i,k] ~ BernoulliLogit(leL1)
leL2 = αL2 + αtL2[k-1] +
βL2[1]*L1[i,k] + βL2[2]*L3[i]
L2[i,k] ~ BernoulliLogit(leL2)
leA = αA + αtA[k-1] +
βA[1]*A[i,k-1] + βA[2]*L1[i,k] +
βA[3]*L1[i,k-1] + βA[4]*L3[i]
A[i,k] ~ BernoulliLogit(leA)
leY = αY + αtY[k] +
βY[1]*A[i,k] + βY[2]*A[i,k-1] +
βY[3]*L1[i,k] + βY[4]*L1[i,k-1] +
βY[5]*L2[i,k] + βY[6]*L2[i,k-1] +
βY[7]*L3[i]
Y[i,k] ~ BernoulliLogit(leY)
end
end
return (L1 = L1, L2 = L2, L3 = L3, A = A, Y = Y)
endI won't do much testing in this post as it's quite time-consuming. But we can take a quick look on the prior predictive distribution of the outcome \(Y\).
unobserved_data = (
L1 = Matrix{Union{Missing, Int}}(missing, 100, 7),
L2 = Matrix{Union{Missing, Int}}(missing, 100, 7),
L3 = Vector{Union{Missing, Int}}(missing, 100),
A = Matrix{Union{Missing, Int}}(missing, 100, 7),
Y = Matrix{Union{Missing, Int}}(missing, 100, 7)
)
priors = sample(
pooled_logit_hazard(100, 7, unobserved_data...),
Prior(),
100
)Here are a sample of risk functions that the priors allow.
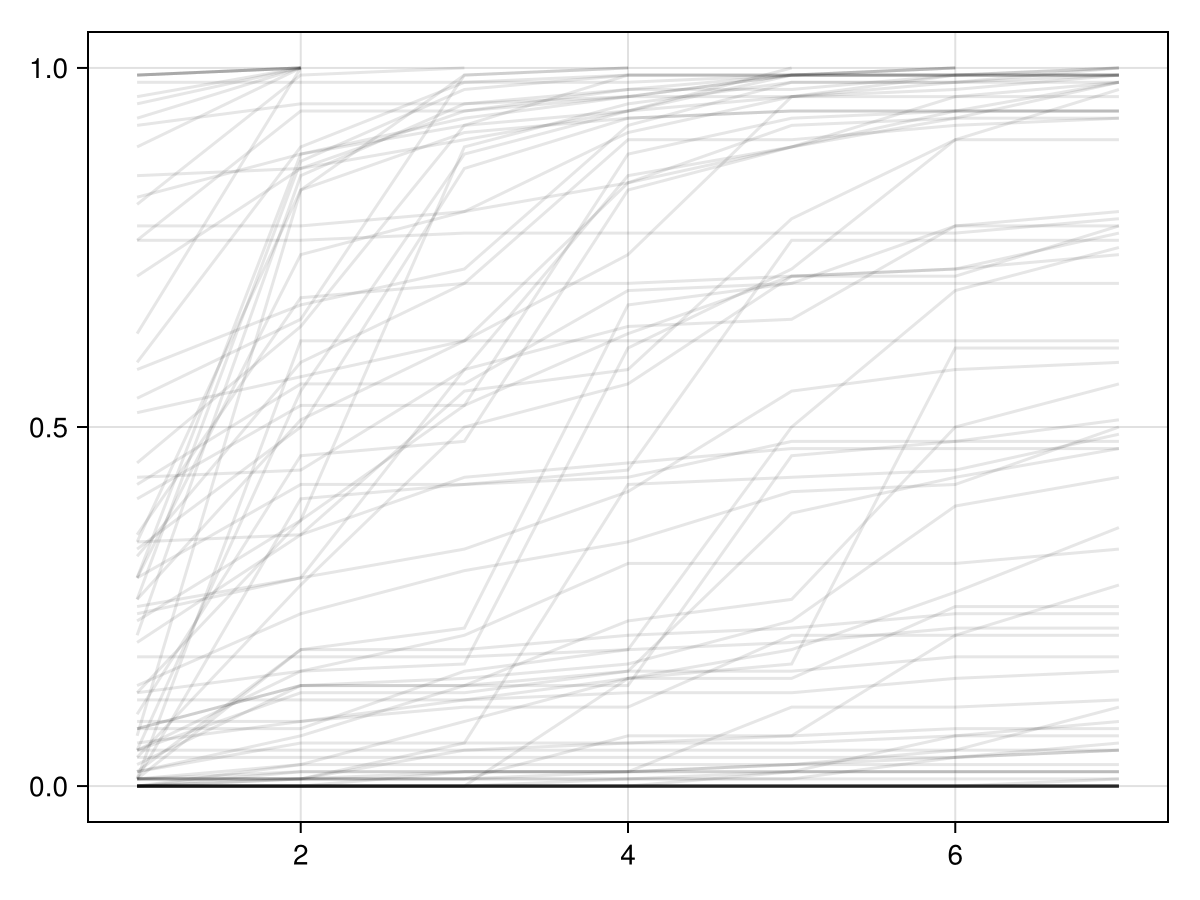
We can also simulate data with some fixed parameter values and check the posterior predictive distribution of the outcome \(Y\) conditional on the simulated dataset.
fixedmodel = fix(
pooled_logit_hazard(100, 7, unobserved_data...),
(
p₁ = fill(0.25, 4),
αL1 = logit(0.5),
αL2 = logit(0.5),
αA = logit(0.5),
αY = logit(0.05),
# Simplest case: Zero coefficients all over.
αtL1 = fill(0, 6),
αtL2 = fill(0, 6),
αtA = fill(0, 6),
αtY = fill(0, 7),
βL1 = fill(0, 2),
βL2 = fill(0, 2),
βA = fill(0, 4),
βY = fill(0, 7),
)
)
simdata = fixedmodel()
preds_given_sim = predict(
pooled_logit_hazard(100, 7, unobserved_data...),
posts_given_sim
)Here's the whole posterior distribution of risk functions from the model fitted on the simulated dataset.
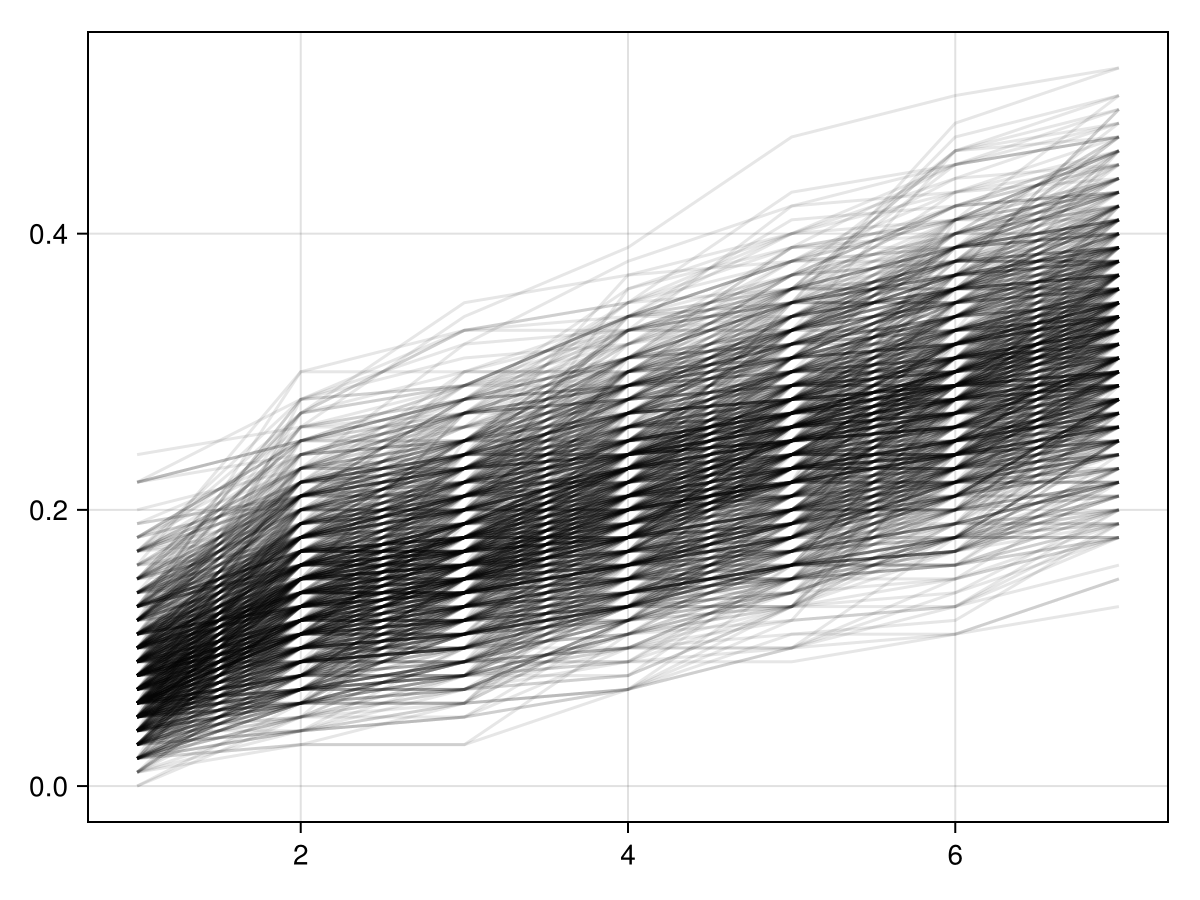
At inference time, we would simulate the fitted/learned model given initial values of covariates (A,L) and either the treatment strategy \(g_1\) or \(g_0\) and then compute the effect measure as a difference of the two posterior predictions. Given all the assumptions, this estimate would then have the causal interpretation we have been targeting for. (Note that only this estimate has a causal interpretation – not the model coefficients or anything else.)
The generated_quantities or predict functions do the job in Julia's Turing library.
Then we would perform the planned robustness checks.
I might make this toy example more complete over time. This is it for now.

